Strong versus Weak Interpolation |
Introduction & Background:As described before, the FreeType 2 Auto-hinter computes segments and edges to model stems and serifs in a given glyph. Edges are grid-fitted relative to each other in order to ensure low distorsion while ensuring stem width normalization. When this first step of alignment control is achieved, points of the glyph outlines must be moved to a new position, depending on their coordinates relative to the edges. For example, all the points that are part of a segment or an edge are moved to the segment/edge's new position, directly. There are however several ways to position/interpolate the remaining points, and they will be explained here. Each interpolation scheme happens in a single dimension at a time. For the sake of clarity, we will consider that we are moving points in the horizontal direction, relative to vertical edges. Strong InterpolationIn the master/font outline, a point that is located between two edges has a coordinate that can be considered a weighted average of its surrounding edge's positions. Strong interpolation consists simply in reproducing this relationship in pixel space, using the grid-fitted position of edges. More technically, the point's pixel position will be the same weigthed average of the grid-fitted edge's positions, using the formula:
p the point to be interpolated
a the edge before the point
b the edge after the point
grid-fitted coordinates are marked with a (')
p.x' = a.x' + ( p.x - a.x ) * ( b.x' - a.x' )/( b.x - a.x )
Also, all points that are before the first edge will be shifted by a distance that corresponds to the edge displacement between its scaled and grid-fitted coordinate. Similarly, each point that is adter the last edge will be shifted by a similar distance computed for the last edge. Note that strong interpolation is equivalent to the TrueType "IP" instruction (which isn't patented btw). Strong interpolation works wonders when it interpolates sections of glyphs that are contained within two edges. However, it can unpleasantly transform sections that span over more than two edges. For example, the contour of the "9" in the following image is "broken", given that some of its control points are incorrectly interpolated (horizontal edges displayed):  Moreover, it is pretty ignorant of the general shape of the glyph and its contours, which can lead to incorrect alignments in the case of overlapping stems positions, as demonstrated by the top dot of the semi-column in the following picture (vertical edges displayed): 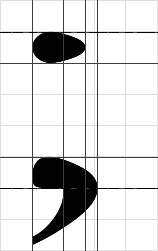 Weak InterpolationWeak interpolation is very similar to strong interpolation, with the exception that instead of taking the position of surrounding edges to compute a weighted average, it takes for each point, the position of the previous and next contour points that have been already "touched". When only one point of the contour is touched, then the whole contour is shifted. When no point of the contour is touched, the contour doesn't move from its scaled position. Weak interpolation works wonders when all extrema points lie on segments and edges. However, it has many weaknesses when this condition isn't met. For example, the following picture shows an "8" whose points have been weak-interpolated (horizontal edges displayed): The problem here is that the inside contours have been simply shifted when the top and bottom stems of the "8" have been aligned. This is due to the fact that only one of their points is touched for each of them. Unfortunately, each inside contour has a vertical extremum that seems to need to be strong-interpolated. Weak interpolation is thus a technique that cannot be used alone. Note that weak interpolation is equivalent to the TrueType "IUP" instruction, which isn't patented. Actually, most TrueType glyph programs hint a glyph through a series of edge alignment + strong interpolation, and call IUP to interpolate the remaining points as the last instruction before the hand-edited delta instructions. Interpolation in FreeType 2Well, as you may have already guessed :o), we use a combination of these two techniques when interpolating point in the FreeType 2 auto-hinter. To be exact, we select which interpolation to apply depending on each point's status, given that not all points are equal. Actually, given that the artefacts of strong interpolation are mostly noticeable when we interpolate bezier control points as well as on-points that define the junction of two tangent arcs or segments, we simply preferably weak-interpolate such points, leaving the others to strong interpolation. We also perform strong interpolation before weak interpolation. This means the following scheme:
|